The purpose of a degree audit is to determine how satisfactorily a student is progressing toward the requirements for graduation within a degree track and major. The general challenge here is to define the degree track specifications in such a way that they can be used to automatically identify a student’s current state of progression and what remains to be done to assure that the student will have passed the necessary courses by the expected graduation date.

There are four requirements in providing any automated solution to the degree audit problem:

Flexibility of Function – The solution must have the flexibility to specify all the requirements necessary for graduation in any of the potential tracks, as automating anything short of the complete requirements is of little value.

Reusability of Components – Because so many degree tracks have major common components, it is necessary to specify those common components only once and then have a way of assembling them into the final requirements.

Clarity of Definition – Because of the complexity of the process and the necessary accuracy of the result, the solution must provide an interface that identifies the requirements in a way that is clear to those doing the specification.

Readability of Results – Since it is the objective of the solution to be effectively read by advisors and students, as well as staff, the results must be as simple and readable as possible, while presenting all the necessary complexities of the requirements.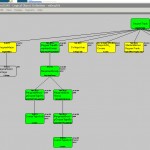

Thus, the first challenge is to determine a structure that has the flexibility and simplicity to meet the objectives above. This is where the AOA structure begins to demonstrate its value. After initial reflection, it is clear that course requirements can be separated into groups with different requirement rules. It is thus natural to construct an object as composed of Course entities within Group entities, as diagrammed to the right. Wrestling with some of the more complex requirements leads to a further need to define a group within a group for these rare, but important exceptions.